Skew t 분포의 정의와 특징
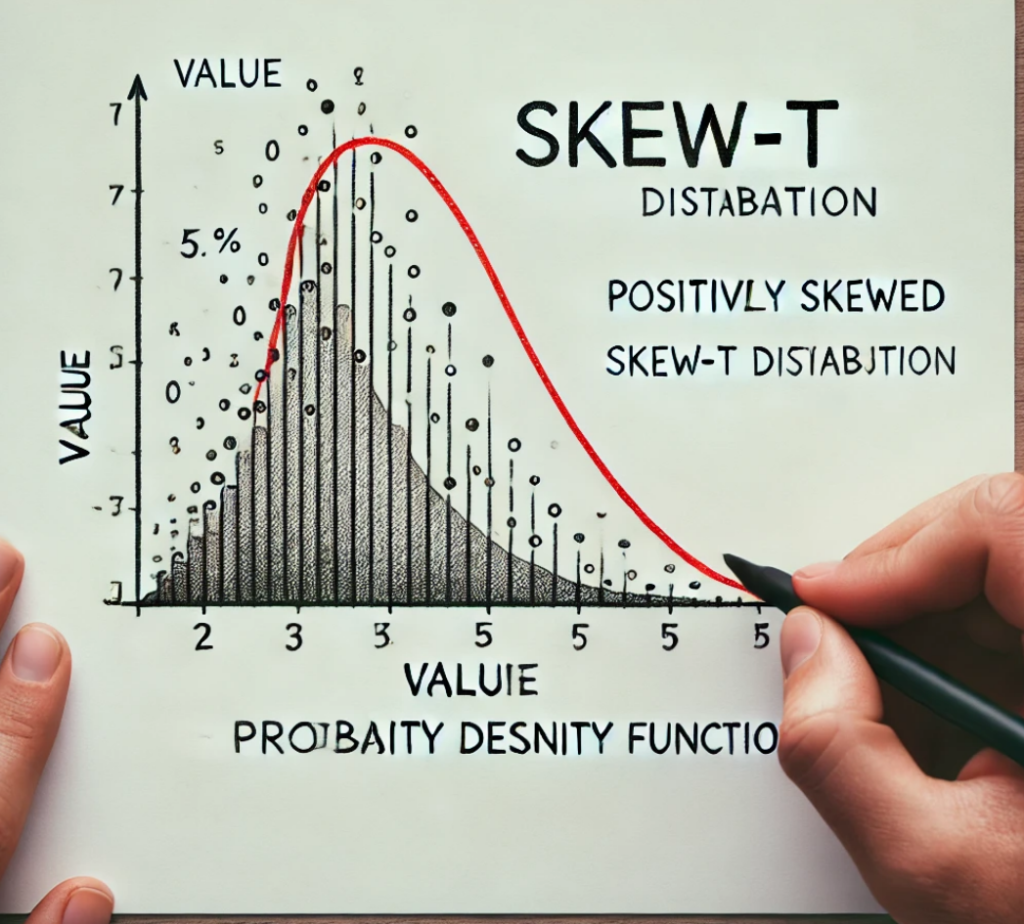
Skew t-분포(Skew t-distribution)는 스튜던트 t 분포의 일반화된 형태로, 비대칭성을 포함하여 분포의 형태를 조정할 수 있습니다. 이 분포는 정규 분포가 비대칭 데이터를 잘 설명하지 못하는 경우에 유용합니다. Skew t 분포는 위치, 척도, 자유도, 비대칭성(스큐니스) 등의 매개변수를 가지고 있으며, 이 매개변수를 통해 다양한 데이터의 특성을 잘 설명할 수 있습니다.
- 위치(Parameter \(\xi\)): 분포의 중심 위치를 나타냅니다.
- 척도(Parameter \(\omega\)): 분포의 확산 정도를 나타냅니다.
- 자유도(Parameter \(\nu\)): 분포의 꼬리 부분의 두께를 결정합니다. 자유도가 높을수록 정규 분포에 가까워집니다.
- 비대칭성(Parameter \(\alpha\)): 분포의 비대칭 정도를 조정합니다. ( \(\alpha\) > 0)이면 오른쪽으로 치우치고, ( \(\alpha\) < 0)이면 왼쪽으로 치우칩니다.
Skew t 분포의 확률 밀도 함수(pdf)
Skew t 분포의 확률 밀도 함수는 복잡한 형태를 가지므로 수식으로 정확하게 표현하기 어렵지만, 일반적으로 비대칭 t 분포의 3차 중심적률(third central moment)을 활용하여 비대칭도를 측정할 수 으며, 3차 중심적률은 비대칭도의 척도인 왜도(skewness)를 계산하는 데 사용됩니다.
비대칭 t 분포의 확률 밀도 함수는 다음과 같이 정의될 수 있습니다:
\[ f(x|\nu, \lambda) = 2 t_\nu(x) T_\nu(\lambda x \sqrt{\frac{\nu+1}{\nu+x^2}}) \]
여기서 \( t_\nu(x) \)는 자유도 \(\nu\)를 가진 표준 t 분포의 밀도 함수이고, \( T_\nu \)는 자유도 \(\nu\)를 가진 표준 t 분포의 누적 분포 함수입니다. \(\lambda\)는 비대칭성을 제어하는 매개변수입니다.
3차 중심적률을 계산하려면, 비대칭 t 분포의 확률 밀도 함수를 이용하여 다음과 같은 적분을 계산합니다:
\[ \mu_3 = E[(X – \mu)^3] = \int_{-\infty}^{\infty} (x – \mu)^3 f(x|\nu, \lambda) dx \]
이 적분의 구체적인 해석적인 계산은 매우 복잡할 수 있으며, 일반적으로 수치적 방법을 사용하여 계산합니다. 그러나 왜도를 정의하는 3차 중심적률을 통해 비대칭 t 분포의 왜도를 구할 수 있습니다.
왜도는 다음과 같이 정의됩니다:
\[ \text{왜도} = \frac{\mu_3}{\sigma^3} \]
여기서 \(\mu_3\)는 3차 중심적률, \(\sigma\)는 표준편차입니다.
비대칭 t 분포의 경우, 왜도는 비대칭성 매개변수 \(\lambda\)에 의존하며, 이는 비대칭성을 설명하는 데 중요한 역할을 합니다.
\[ f(x; \xi, \omega, \nu, \alpha) = 2 \cdot t\left(\frac{x – \xi}{\omega}; \nu\right) \cdot T\left(\alpha \cdot \left(\frac{x – \xi}{\omega}\right) \cdot \sqrt{\frac{\nu + 1}{\nu + (x – \xi)^2 / \omega^2}}; \nu + 1\right) \]
여기서 ( t는 자유도가 \(\nu\)인 표준 t 분포의 확률 밀도 함수이고, ( T )는 자유도가 (\(\nu\))인 표준 t 분포의 누적 분포 함수입니다.
Skew t 분포의 활용
Skew t 분포는 금융 데이터 분석, 생명과학, 공학 등 다양한 분야에서 비대칭성을 고려한 데이터 분석에 사용됩니다. 특히, 극단값이나 비대칭적인 데이터를 모델링할 때 유용합니다.
■ Python을 이용한 스큐 t 분포 시뮬레이션
matplotlib 설치
pip install matplotlib
우선 실행해
정상 설치 완료 시
Python에서는 “scipy”라이브러리와 “statsmodels” 라이브러리를 사용하여 스큐 t 분포를 시뮬레이션할 수 있습니다.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import skewnorm, t
# 매개변수 설정
alpha = 5 # 비대칭성
df = 10 # 자유도
loc = 0 # 위치
scale = 1 # 척도
# 스큐 t 분포 데이터 생성
data = t(df, loc=loc, scale=scale).rvs(1000) + skewnorm(alpha, loc=loc, scale=scale).rvs(1000)
# 히스토그램 그리기
plt.hist(data, bins=30, density=True, edgecolor='black', alpha=0.7)
plt.title('Histogram of Skew t Distribution')
plt.xlabel('Value')
plt.ylabel('Density')
plt.show()위 코드는 스큐 t 분포를 시뮬레이션하여 히스토그램으로 시각화한 것입니다. “scipy.stats”모듈의 ” skewnorm”함수와 t 함수를 사용하여 비대칭성과 자유도를 조절한 데이터를 생성합니다.
스큐 t 분포는 데이터의 비대칭성을 포함하여 다양한 분포 형태를 설명할 수 있는 유용한 도구로, 이를 통해 복잡한 데이터를 보다 정확하게 모델링할 수 있습니다.
■ Skew t-distribution in R
R 프로그래밍에서는 “skew-t”분포를 시뮬레이션하고 분석하기 위해 다양한 패키지를 사용할 수 있습니다. 대표적으로 “sn” 패키지가 있으며, 이 패키지는 스큐 t 분포를 포함한 여러 스큐 분포를 다룰 수 있는 기능을 제공합니다.
다음은 “sn” 패키지를 사용하여 스큐 t 분포를 시뮬레이션하고, 이를 시각화하는 예제 코드입니다.
1. SN 패키지 설치 및 로드
# 패키지 설치
install.packages("sn")
# 패키지 로드
library(sn)
2. Skew t 분포 데이터 생성
R 에서 ‘rst’함수 활성화 하기 위하여
우선
library(sn)
실행
# 매개변수 설정
xi <- 0 # 위치 (location)
omega <- 1 # 척도 (scale)
alpha <- 5 # 비대칭성 (skewness)
nu <- 10 # 자유도 (degrees of freedom)
# 스큐 t 분포 데이터 생성
set.seed(123) # 재현성을 위해 시드 설정
data <- rst(n=1000, xi=xi, omega=omega, alpha=alpha, nu=nu)3. 히스토그램 및 밀도 함수 시각화
# 히스토그램 그리기
hist(data, breaks=30, probability=TRUE, main="Histogram of Skew t Distribution", xlab="Value", col="lightblue", border="black")
# 밀도 함수 추가
lines(density(data), col="red", lwd=2)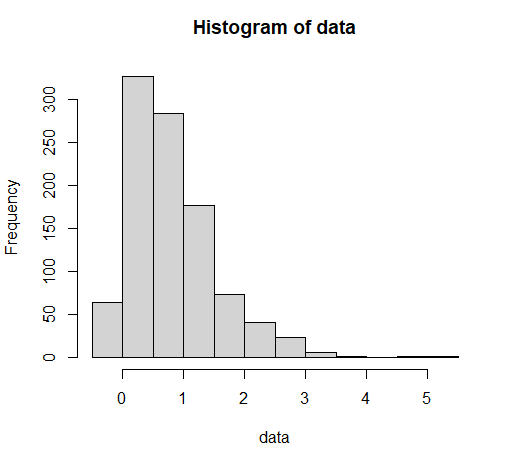
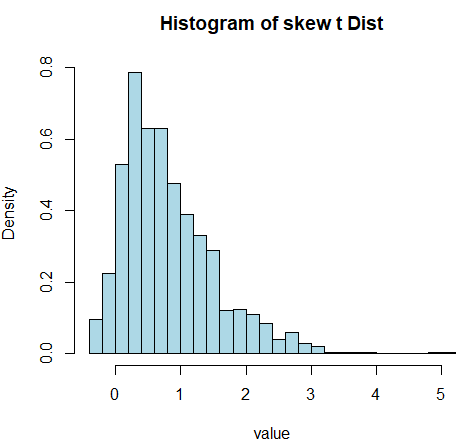

4. Skew t 분포의 밀도 함수와 누적 분포 함수 그리기
# 밀도 함수
x <- seq(-5, 5, length=100)
y_density <- dst(x, xi=xi, omega=omega, alpha=alpha, nu=nu)
# 밀도 함수 시각화
plot(x, y_density, type="l", col="blue", lwd=2, main="Density Function of Skew t Distribution", xlab="Value", ylab="Density")
# 누적 분포 함수
y_cdf <- pst(x, xi=xi, omega=omega, alpha=alpha, nu=nu)
# 누적 분포 함수 시각화
plot(x, y_cdf, type="l", col="green", lwd=2, main="CDF of Skew t Distribution", xlab="Value", ylab="Probability")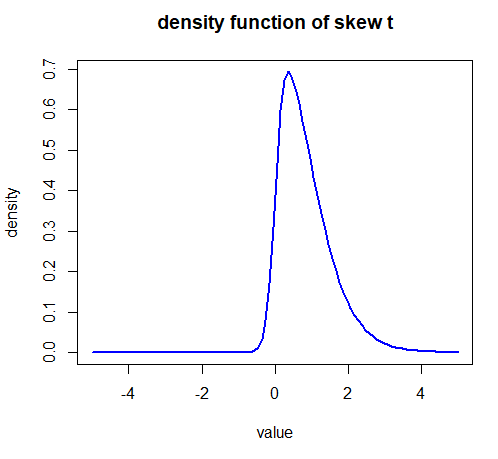
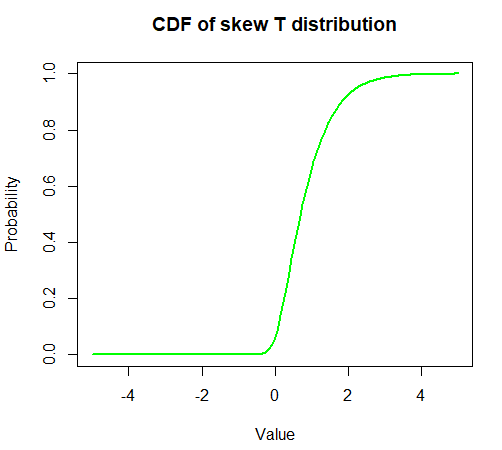
위의 코드는 “sn” 패키지를 사용하여 스큐 t 분포 데이터를 생성하고, 그 히스토그램과 밀도 함수를 시각화하는 예제입니다. 또한, 밀도 함수와 누적 분포 함수도 각각의 그래프로 시각화합니다.
5. R 코드를 통해 이해한 내용 요약
- 패키지 설치 및 로드: “sn”패키지를 설치하고 로드
- 데이터 생성: “rst”함수를 사용하여 스큐 t 분포 데이터를 생성
- 히스토그램 시각화: 히스토그램을 그려 데이터 분포를 시각적 확인
- 밀도 함수와 누적 분포 함수 시각화: “dst”와 “pst” 함수를 사용하여 각각 밀도 함수와 누적 분포 함수를 계산 및 시각화

